PRODUCT SMART UQ
実験計画法(Design of Experiments: DOE)
実験の並列最適ラテン超立方体計画。
当社の最先端のDOEは、必要なポイント数を減らしながら、十分なサンプリングを保証します。当社独自のDOEはさらに進んで、以前にサンプリングされたポイントからの情報を使用して、次のサンプルを取得する場所を決定し、前進するために必要なデータを提供します。大規模な観測データセットからサブサンプリングすることで、既成概念にとらわれずに考えることもできます。さらに、SmartUQの柔軟なDOE生成ツールを使用すると、特定のニーズに合わせてサンプリングを調整できます。
1つ確かなことは、DOEを設計するためにSmartUQソフトウェアを選択すると、実行回数が大幅に減り、より正確で包括的な結果が得られるため、時間と費用の両方を節約できます。
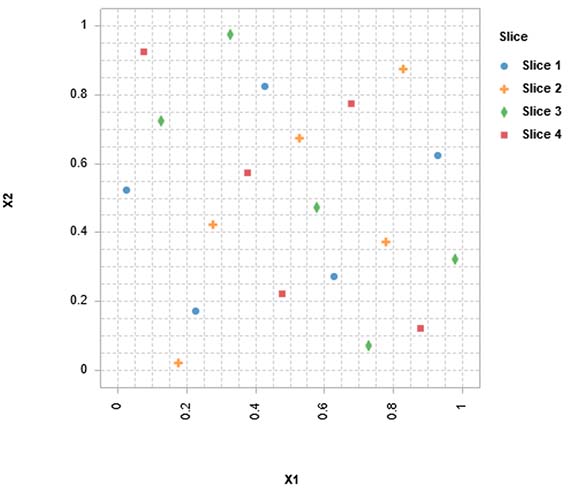
実験計画法(DOE)とは
実験計画法(DOE)とは、入力と出力の間の原因と結果の関係を明らかにするための実験を行う際に使用される体系的なサンプリングパターンです。適切な実験から十分な情報を収集するためのDOEがなければ、テストの目的を達成することが困難または不可能になる可能性があります。実験者やシミュレーションユーザーの直感に頼ったサンプリングパターンを使ってシミュレーションやテスト実験を行うと、入力がどのように相互作用するのかが理解できず、テストリソースの無駄遣いや機会損失につながる可能性があります。
このような問題を解決するには、複数の要因を同時に変化させる多因子を考慮した実験計画法を用いることが有効です。個々の要因の影響だけでなく、様々な要因のペアや組み合わせがどのように相互作用して出力値を変化させるかを評価することが重要です。
空間充填型のDOE
要因計画法のようなDOEは強力な情報収集能力を備えていますが、非線形性の高いシステムの原因と結果の関係を判断するためには、必要以上のサンプルを多額の費用をかけて採取する必要があることがよくあります。最新の空間充填型のDOEは、非線形性の高い応答を伴うシミュレーションや複雑な物理実験において、最も効率的なDOEであることが多いです。
ラテン超方格法や最適化ラテン超方格法などの空間充填型DOEでは、一連の代表的な入力設定を均等に分散してサンプリングし、設計空間を充填します。このタイプのDOEでは,シミュレーションの回数を最小限に抑えながら,各シミュレーションから得られる潜在的な学習効果を最大限に高めることができるという研究結果が出ています.このように、空間充填型DOEは、サンプリングポイントの総数を減らしながら、高い精度を実現します。
シーケンシャルおよびマルチフィデリティDOE
シーケンシャルおよびマルチフィデリティDOE
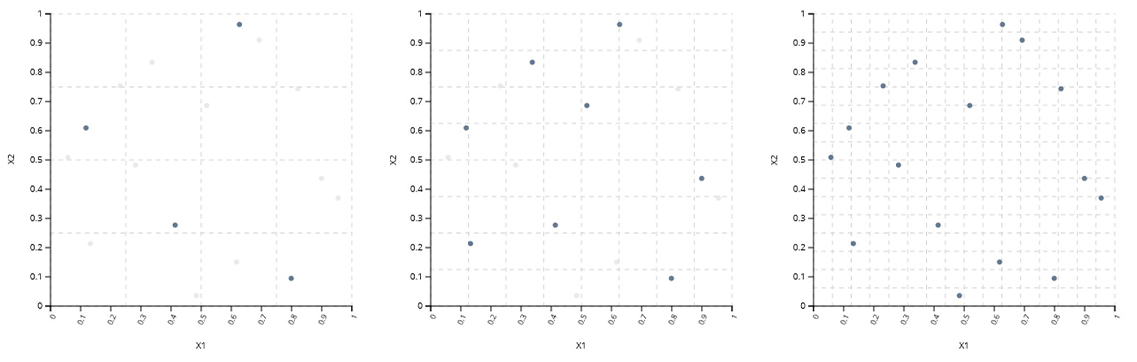
シーケンシャルDOE
この例では、最初に4点のDOEが生成されます。続いて、2番目の4点DOE、3番目の8点DOEが生成され、最初のDOEの分解能を順次高めていきます。
並列の空間充填型DOE
並列DOEでは、サンプリングポイントを別々の並列バッチに分割します。これは、連続的な入力と離散的な入力が混在している場合に特に有効で、各バッチで離散的な入力を個別に扱うことができます。また、各バッチをより小さな並列DOEで構成することで、複数の離散的な入力に対応することも可能です。
これらのDOEは、計算や実験の作業を複数のグループに分割する際にも有効です。コンピュータ実験では、実験全体の計算負荷をより大きなグループのコンピュータデバイスに分割することで、クロックタイムを大幅に削減することができます。
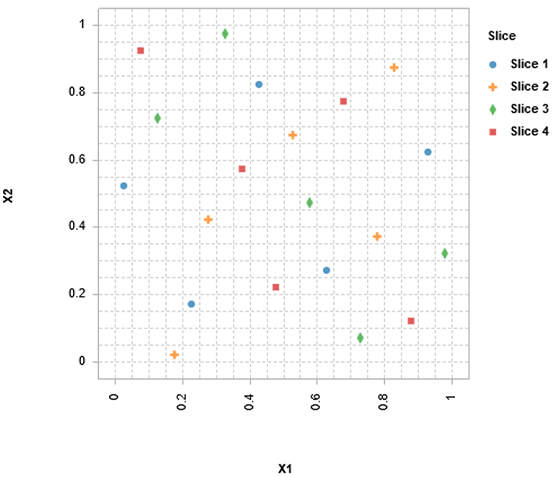
並列DOE
この例では、2つの連続入力と4つのレベルを持つ1つの離散入力を扱うのに適した、最適な2次元、20ポイント、4バッチのDOEを示しています。
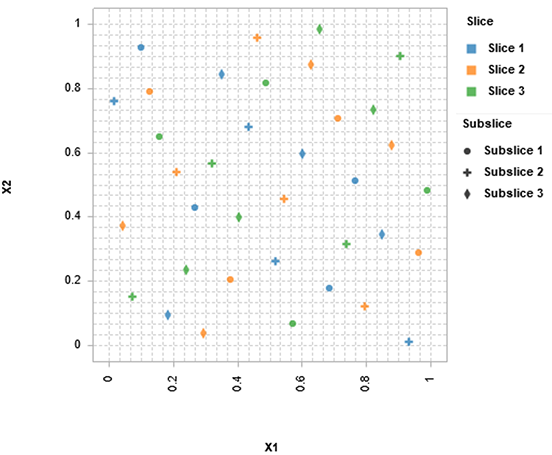
二重並列
この例では、2つの連続した入力と、それぞれ3レベルの2つの離散的な入力を扱うのに適した、2次元、36点、2重並列のDOEを示しています。
適応型DOE
適応型DOEでは、エミュレータの作成に使用したDOEに適応的にポイントを追加することで、フィットしたエミュレータ(サロゲートモデル、メタモデル)の精度を高めることができます。このプロセスでは、既存のDOEと関連する結果データからエミュレータを作成します。次に、このエミュレータを用いて、エミュレータの精度を高めるために、次のシミュレーションをどこに追加すべきかを判断します。このプロセスは、望ましいレベルのフィッティング精度が得られるまで繰り返すことができます。
以下にいくつかの難しい特徴を持つ応答曲面を、1度で済ます最適ラテン超方格法DOEと適応型DOEの2つの手法を用いたアルゴリズムでエミュレートした例を紹介します。
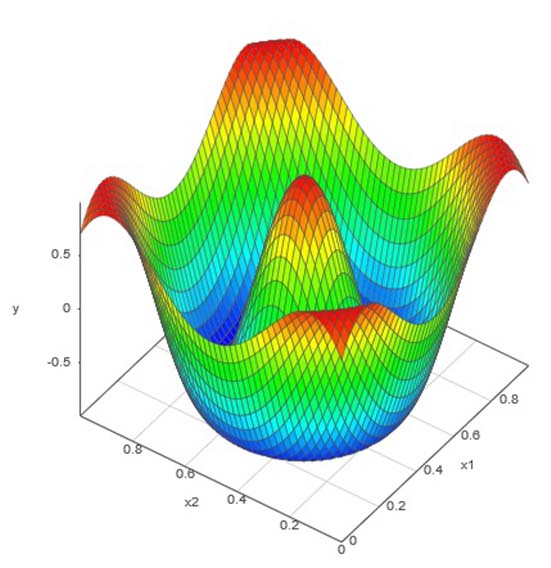
応答曲面
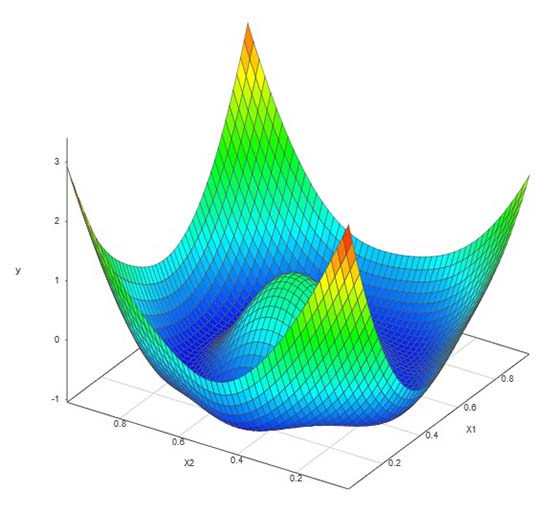
一度に行った最適ラテン超方格法(LHD)
2つ目のDOEは、当社独自の適応型DOEです。SmartUQの適応型DOEの機能は、最初に20ポイントの最適なLHDを設定した後、設計空間に5ポイントを1つずつ追加していきました。各ポイントは、前回のエミュレータに基づいて当社のアルゴリズムが選択した設計空間の特定の領域を対象としています。このアプローチにより、同じ数のシミュレーションを実行しながらも、誤差を1桁減らすことができ、より正確なモデルを得ることができました。
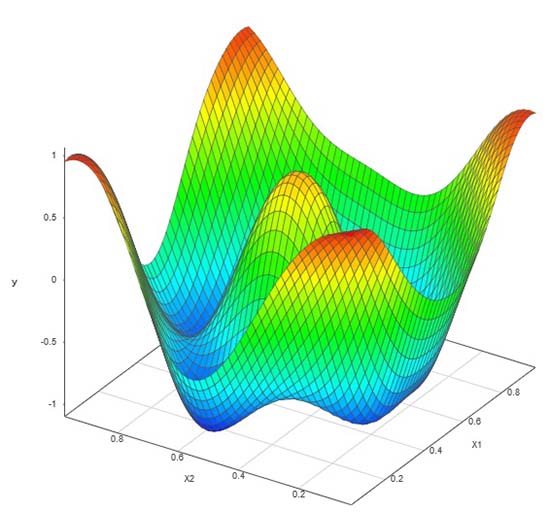
適応型DOE
拡張型DOE(Design Augmentation)
拡張型DOE(Design Augmentation)では、既存のDOEと組み合わせてDOEを生成し、新しいポイントが組み合わせたDOEの空間充填の特性を最大化することができます。実際には、大規模なDOEに必要なすべての設計点を1回のシミュレーションで実行することは望ましくない、または実行不可能な場合があります。また、以前の設計空間の調査、最適化手順、製品開発サイクルなどで作成した既存のDOEがあることもよくあります。これらのDOEは、空間を埋めるのに適していないかもしれませんが、貴重な情報を含んでいます。設計空間の拡張は、過去に収集したデータを活用しつつ、一定回数の新規シミュレーション実行から得られる情報を最大化するために必要な、最適なシミュレーション実行を決定するのに有効です。
拡張型DOEは適応型DOEとは異なります。拡張型DOEでは、既存のDOE自体の特性に基づいて、最適なポイントが生成されます。そのため、新しいポイントはシミュレーション結果からは見えません。適応型DOEでは、最適なポイントは、DOEの特性だけでなく、以前のシミュレーション結果を用いて作成されたエミュレーターに基づいて生成されます。拡張型DOEは適応型DOEよりもロバスト性に優れていますが、これは適応型DOEがモデルフリーであり、任意の数のレスポンスを持つシミュレーションに対応しているためです。拡張型DOEと適応型DOEはどちらも有用な補完ツールであり、ユーザーは研究対象となる特定のケースの特性に基づいてこれらの2つのオプションを決定する必要があります。
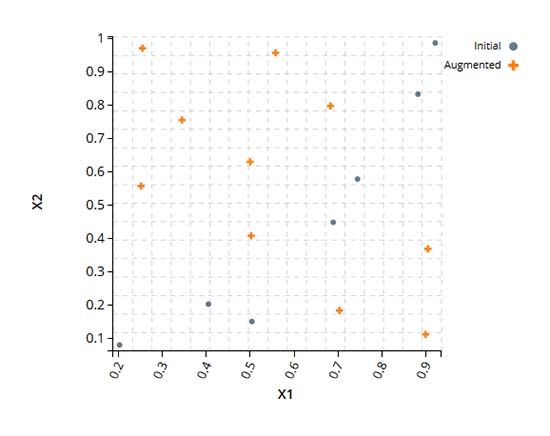
拡張されたDOE
この例では、品質の低い初期のDOEを補強して、設計空間全体をカバーするDOEを作成しています。
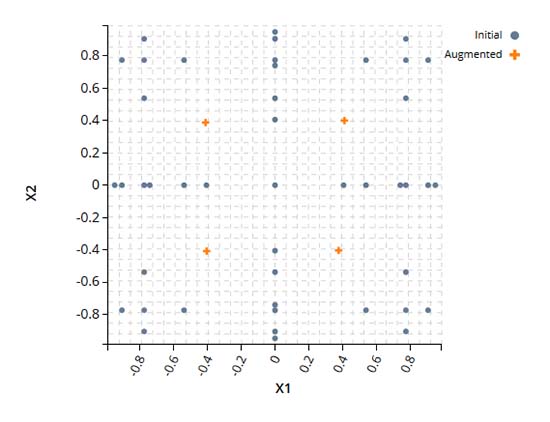
スパースグリッド
この例では、シミュレーションの収束に失敗したためにデータが欠落したスパースグリッドを補強し、DOEの空間充填特性を向上させています。この機能は、データが欠けているために多項式カオスに基づく不確かさの解析が行えない場合に特に有効です。
データサンプリング
DOEは通常、システムから新しいデータを収集するために使用されます。多くの場合、十分なデータがすでに揃っています。このようなシナリオでは、収集されたデータが長期間にわたって蓄積されており、解析が困難なほど十分なデータがあることがよくあります。例えば、現場で使用されている部品のセンサーからのヘルスモニタリングデータは、その部品の動作寿命全体にわたって継続的にライブ・データを取得している場合があります。SmartUQのデータサンプリングツールは、データを分割し、全データセットのサブセットで構成される空間充填DOEを模倣することができます。データ収集前に作成されるDOEとは異なり、サブサンプリングやスライスサンプリングなどのデータ・サンプリングでは、既存の入出力データペアを使用して、設計空間をうまく表現するポイントを選択します。